Answer:
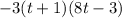
Explanation:
First, factor both the denominators completely:
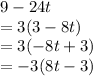
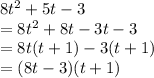
Now, we can see that the factors of the first denominator are -3 and 8t-3.
The factors of the second denominator are t+1 and 8t-3.
To find the LCD, multiply all of these factors together:
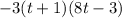
Notice how we only multiply 8t-3 in the equation once. This is because it was present in both denominators, unlike the other factors.
I hope this helps!