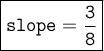To find the slope of a line, we can use the following formula:

m-term stands for slope or gradient. The formula is useful whenever you want to find a slope of two points.
Let these be the following:
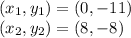
Substitute the points in formula:
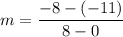
Negative multiply negative always come out as positive.
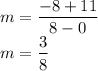
Since m stands for slope, we can say that: