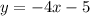Question

(SHOW WORK) Write the slope-intercept form of the equation:

passes through (-2, 3) and is perpendicular to y = 1/4x - 4

Answer 1

`\displaystyle y = -4x - 5`

Explanation:

We want to find the slope-intercept form of the equation that passes through the point (-2, 3) and is perpendicular to the line:

`\displaystyle y = (1)/(4) x - 4`

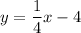
Note that this line has a slope of 1/4.

Recall that the slopes of perpendicular lines are negative reciprocals of each other.

Since the slope of our old line is 1/4, the slope of its perpendicular line must be -4.

We are also given that it passes through the point (-2, 3). So, we can consider using point-slope form:

`\displaystyle y - y_1 = m(x - x_1)`

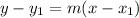
Let (-2, 3) be (x₁, y₁) and substitute -4 for the slope m. Hence:

`\displaystyle y - (3)= -4 (x - (-2))`

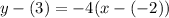
Convert into slope-intercept form. Simplify:

`\displaystyle \begin{aligned} y -3 &= -4 (x + 2) \\ y - 3 &= -4x - 8 \\ y &= -4x -5\end{aligned}`

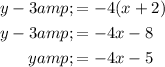
In conclusion, the perpendicular line that passes through the point (-2, 3) is given by:

`\displaystyle y = -4x - 5`