Answer:
The statement in the question is wrong. The series actually diverges.
Explanation:
We compute
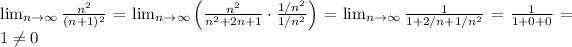
Therefore, by the series divergence test, the series
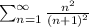 diverges.
diverges.
EDIT: To VectorFundament120, if
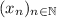 is a sequence, both
is a sequence, both
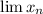 and
and
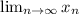 are common notation for its limit. The former is not wrong but I have switched to the latter if that helps.
are common notation for its limit. The former is not wrong but I have switched to the latter if that helps.