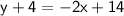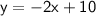Answer:
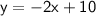
Explanation:
slope-intercept form of a linear equation: y = mx + b
(where m is the slope and b is the y-intercept)
point-slope form of a linear equation:
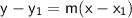
(where m is the slope and
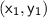 is the point)
is the point)
Given:
- m = -7
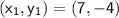
Substitute these values into the point-slope equation:
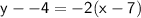
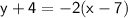
Now rearrange to put into slope-intercept form by making y the subject: