Answer:
 .
.
Explanation:
The diagram suggests that the length of a row of five cubes is
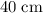 . Hence, the length of the edge of each cube would be:
. Hence, the length of the edge of each cube would be:
 .
.
That would correspond to an area of
 for each face of the cube.
for each face of the cube.
Refer to the diagram attached.
Viewing from the front and from the rear each shows
 faces of the cubes.
faces of the cubes.
Viewing from the top and from the bottom each shows
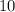 faces of the cubes.
faces of the cubes.
Viewing from the left and from the right each shows
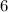 faces of the cubes.
faces of the cubes.
When viewed from the six perspectives,
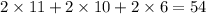 faces of the cubes are visible in total.
faces of the cubes are visible in total.
For this particular construction, all faces that need to be painted are visible when viewed from exactly one of the six perspectives: front, rear, top, right, left, right. Hence, Sam would need to paint
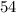 of such
of such
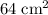 squares.
squares.
The area that Sam needs to paint would be
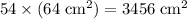 .
.