Answer:
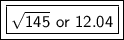
Explanation:
The distance between 2 points is calculated using the following formula.
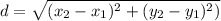
In this formula, (x₁, y₁) and (x₂, y₂) are the coordinates of the two points.
We know the two points are (4, -9) and (5,3). If we match the values of the points and the coordinating variable, we see that:
- x₁ = 4
- y₁= -9
- x₂ = 5
- y₂ = 3
Substitute the values into the formula.
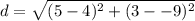
Solve inside the parentheses.
- (5-4)= 1
- (3 --9) = (3+9) = 12
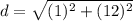
Solve the exponents.
- (1)² = 1 *1 = 1
- (12)² = 12 * 12 = 144
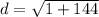
Add.
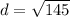
Take the square root.
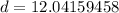
Let's round to the nearest hundredth. The 1 in the thousandth place tells us to leave the 4 in the hundredth place.
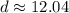
The distance between the 2 points is √145 or approximately 12.04.