Question

Someone please help.

Answer 1

Hi there!

`f(x)+f(x+1)=4f(x)`

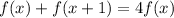
There are 3 parts to this equation:

f(x)

f(x+1)

4f(x)

We must first determine these three parts separately.

1) f(x)

We're given that
`f(x)=3^x`:

⇒
`f(x)=3^x`:

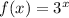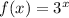2) f(x+1)

Now, we must find f(x+1). To do so, add 1 to x in the original function
`f(x)=3^x`:

⇒
`f(x+1)=3^x^+^1`

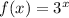3) 4f(x)

To find 4f(x), multiply the original function
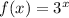`f(x)=3^x` by 4:

`4f(x)=4*3^x`:

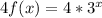4) Put it all together

Now, plug each of the three parts into the equation
`f(x)+f(x+1)=4f(x)`:

`f(x)+f(x+1)=4f(x)`

`3^x+3^x^+^1=4*3^x\\3^x+3^x*3=4*3^x`

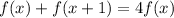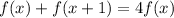
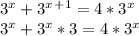
Factor the left side

`3^x*(1+3)=4*3^x`

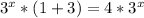
Divide both sides by 3^x

`1+3=4\\4=4`

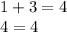
Because this equation is true,
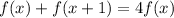`f(x)+f(x+1)=4f(x)` is therefore true.

I hope this helps!