Question

Find all values of c such that 3^2c+1=28*3^c-9. If you find more than one value of c, then list your values in increasing order​

Answer 1

`3^(2c) + 1 = 28*3^c - 9 \implies 3^(2c) - 28*3^c = -10`

Complete the square on the left side:

`3^(2c) - 28*3^c = \left(3^(2c)-28*3^c+14^2\right)-14^2 = \left(3^c-14\right)^2 - 196`

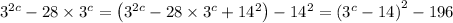
Then the equation becomes

`\left(3^c-14\right)^2 - 196 = -10 \\\\ \left(3^c-14\right)^2 = 186 \\\\ 3^c - 14 = \pm√(186) \\\\ 3^c = 14\pm√(186)`

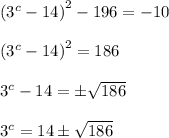
Both 14 + √186 and 14 - √186 are positive numbers, so we can take the logarithm (base 3) of both sides without issue:

`\log_3\left(3^c) = c = \log_3\left(14\pm√(186)\right)`

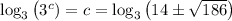
Then in increasing order, the solutions are

c = log₃(14 - √186), c = log₃(14 + √186)