It looks like the limit you want to compute is
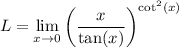
Rewrite the limand with an exponential and logarithm:
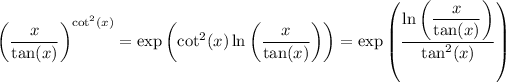
Now, since the exponential function is continuous at 0, we can write
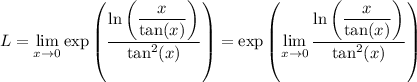
Let M denote the remaining limit.
We have
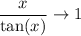 as
as
 , so
, so
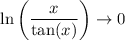 and
and
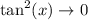 . Apply L'Hopital's rule:
. Apply L'Hopital's rule:
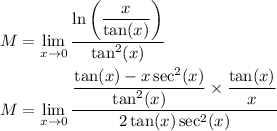
Simplify and rewrite this in terms of sin and cos :
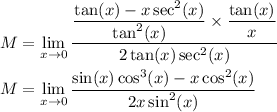
As
 , we get another 0/0 indeterminate form. Apply L'Hopital's rule again:
, we get another 0/0 indeterminate form. Apply L'Hopital's rule again:
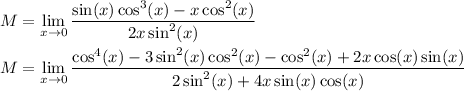
Recall the double angle identity for sin:
sin(2x) = 2 sin(x) cos(x)
Also, in the numerator we have
cos⁴(x) - cos²(x) = cos²(x) (cos²(x) - 1) = - cos²(x) sin²(x) = -1/4 sin²(2x)
So we can simplify M as
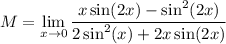
This again yields 0/0. Apply L'Hopital's rule again:
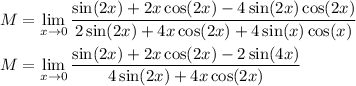
Once again, this gives 0/0. Apply L'Hopital's rule one last time:
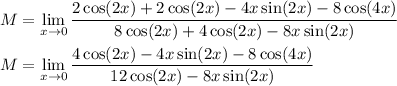
Now as
 , the terms containing x and sin(nx) all go to 0, and we're left with
, the terms containing x and sin(nx) all go to 0, and we're left with
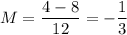
Then the original limit is
![L = \exp(M) = e^(-1/3) = \boxed{\frac1{\sqrt[3]{e}}}](https://img.qammunity.org/2022/formulas/mathematics/college/yb8n8484ghhs8mjf0maa8dsrq37qubol22.png)