Question

Show that there do not exist scalar c1 c2 and c3 c1(-2,9,6)+c2(-3,2,1)+c3(1,7,5)= (0,5,4)​

Answer 1

This is the same as showing the following system of equations doesn't have a solution:

`\begin{cases}-2c_1-3c_2+c_3 = 0 \\ 9c_1 + 2c_2 + 7c_3 = 5 \\ 6c_1 + c_2 + 5c_3 = 4\end{cases}`

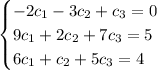
or in matrix form,

`\begin{bmatrix}-2&9&6\\-3&2&1\\1&7&5\end{bmatrix}\begin{bmatrix}c_1\\c_2\\c_3\end{bmatrix} = \begin{bmatrix}0\\5\\4\end{bmatrix}`

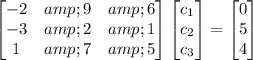
The quickest way to check if there is a solution is to check whether the coefficient matrix is invertible. If its determinant is 0, then it is not invertible.

And the quickest way to show that the determinant is 0 is by observing that the third row is a linear combination of the first two rows:

(-2, 9, 6) - (-3, 2, 1) = (-2 + 3, 9 - 2, 6 - 1) = (1, 7, 5)

So there are indeed no such scalars c₁, c₂, and c₃.