Answer:
Assumption: the acceleration of this vehicle is constant until it comes to a stop.
Acceleration:
 .
.
The acceleration of this vehicle is negative because the velocity of this vehicle is decreasing over time.
Step-by-step explanation:
- Let
 denote the initial velocity of this vehicle.
denote the initial velocity of this vehicle.
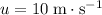 .
. - Let
 denote the final velocity of this vehicle.
denote the final velocity of this vehicle.
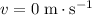 as the vehicle has come to a stop.
as the vehicle has come to a stop. - Let
 denote the displacement of this vehicle.
denote the displacement of this vehicle.
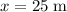 .
. - Let
 denote the acceleration of this vehicle. The value of
denote the acceleration of this vehicle. The value of
 needs to be found.
needs to be found.
Assume that the acceleration of this vehicle,
 , is constant. The SUVAT equations would apply.
, is constant. The SUVAT equations would apply.
The time
 required for braking is neither given nor required. Hence, make use of the SUVAT equation
required for braking is neither given nor required. Hence, make use of the SUVAT equation
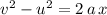 to relate
to relate
 ,
,
 ,
,
 , and
, and
 .
.
Rearrange this equation to find an expression for
 , the acceleration of this vehicle:
, the acceleration of this vehicle:
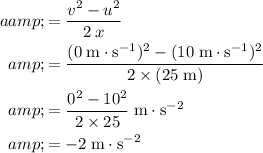 .
.
- When the rate of change of a value is greater than
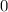 , that value would become larger over time.
, that value would become larger over time. - When the rate of change of a value is equal to
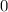 , that value would be constant.
, that value would be constant. - When the rate of change of a value is smaller than
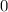 , that value would become smaller over time.
, that value would become smaller over time.
Acceleration is the rate at which velocity changes over time.
The velocity of the vehicle in this question is getting smaller over time. Hence, the rate of change of the velocity of this vehicle (that is, the acceleration of this vehicle) would be a negative number.