Solving for Angles

* Do not forget to use the inverse function towards the end, or elce you will throw your answer off!
Solving for Edges
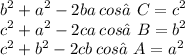
You would use this law under two conditions:
- One angle and two edges defined, while trying to solve for the third edge
- ALL three edges defined
* Just make sure to use the inverse function towards the end, or elce you will throw your answer off!
_____________________________________________
Now, JUST IN CASE, you would use the Law of Sines under three conditions:
- Two angles and one edge defined, while trying to solve for the second edge
- One angle and two edges defined, while trying to solve for the second angle
- ALL three angles defined [of which does not occur very often, but it all refers back to the first bullet]
* I HIGHLY suggest you keep note of all of this significant information. You will need it going into the future.
I am delighted to assist you at any time.