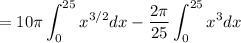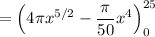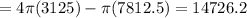Step-by-step explanation:
Let
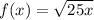 and
and
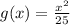 . The differential volume dV of the cylindrical shells is given by
. The differential volume dV of the cylindrical shells is given by
![dV = 2\pi x[f(x) - g(x)]dx](https://img.qammunity.org/2022/formulas/mathematics/college/j7hpxleq2ia158iy7yju774ix6rsyllb99.png)
Integrating this expression, we get
![\displaystyle V = 2\pi\int{x[f(x) - g(x)]}dx](https://img.qammunity.org/2022/formulas/mathematics/college/d4dc35tuvx82i8qkf3646q2crca2dmwq0c.png)
To determine the limits of integration, we equate the two functions to find their solutions and thus the limits:

We can clearly see that x = 0 is one of the solutions. For the other solution/limit, let's solve for x by first taking the square of the equation above:
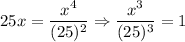
or

Since we are rotating the functions around the y-axis, we are going to use the x = 25 solution as one of the limits. So the expression for the volume of revolution around the y-axis is