Question

Can someone please help me?

Answer 1

The equation of the perpendicular line (PR) to line PQ is; y = -0.5x - 1.5

Explanation:

The line is perpendicular to line adjoined by points P(-3,0) and Q(0,6)

The slope of line PQ is;

Slope = change in y ÷ change in x =
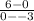`(6 - 0)/(0 -- 3)` = 2

The product of slopes of two perpendicular lines = -1

Hence the slope of line PR = -1 ÷ slope of line PQ = -1/2

Taking another point (x,y) and point P(-3,0) the equation of line PR is;

Slope =
`(y - 0)/(x - -3) = -(1)/(2)`

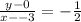
Cross-multiplying gives;

2y = -x - 3 , y = -x/2 - 3/2 , y = -0.5x - 1.5