Solve the equation to find x: 7-3e^x=4

Question

asked Mar 7, 2023 35.5k views

1 Answer

Agrejus · Answer 1 · 2023-03-13T18:28:02+0000

Answer:

x = 0

Explanation:

Given equation:

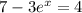
7-3e^x=4

Add 3eˣ to both sides of the equation:

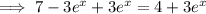
$\implies 7-3e^x+3e^x=4+3e^x$

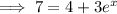
$\implies 7=4+3e^x$

Subtract 4 from both sides of the equation:

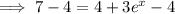
$\implies 7-4=4+3e^x-4$

$\implies 3=3e^x$

Switch sides:

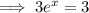
$\implies 3e^x=3$

Divide both sides by 3:

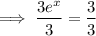
$\implies (3e^x)/(3)=(3)/(3)$

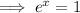
$\implies e^x=1$

Take natural logs of both sides:

$\implies \ln e^x=\ln 1$

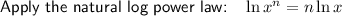
$\textsf{Apply the natural log power law:} \quad \ln x^n=n \ln x$

$\implies x\ln e=\ln 1$

As ln e = 1 and ln 1 = 0:

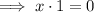
$\implies x \cdot 1=0$

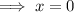
$\implies x =0$

Therefore, the value of x is x = 0.