Question

4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

= Answer should be detailed.​

Answer 1

The height of the parallelogram is 12 cm.

Explanation:

We are given that a triangle and a parallelogram have the same base and same area.

The sides of the triangle measure 26 cm, 28 cm, and 30 cm.

We are given that the base of the parallelogram is 28 cm, and we want to determine its height.

Find the area of the triangle. Since we are given the three sides, we can consider using Heron's Formula:

`\displaystyle A = √(s(s-a)(s-b)(s-c))`

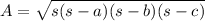
Where a, b, and c are the sides and s is half of the perimeter.

The perimeter is:

`P = (26) + (28) + (30) = 84`

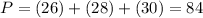
Hence, s = 42.

Then the area of the triangle is:

`\displaystyle \begin{aligned} A&= √(42(42-26)(42-28)(42-30)) \\ &= √(112896) \\ &= 336\text{ cm}^2 \end{aligned}`

The area of a parallelogram is given by:

`\displaystyle A = bh`

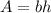
We are given that the base is 28 cm:

`\displaystyle A = 28 h`

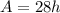
Its area is equivalent to the area of the given triangle. Hence:

`\displaystyle 336 = 28h`

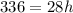
Divide:

`\displaystyle h = (336)/(28) = 12\text{ cm}`

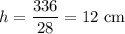
In conclusion, the height of the parallelogram is 12 cm.