Answer:
The vertex is at (-1, -16).
Explanation:
We are given the quadratic equation:
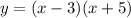
And we want to find its vertex.
Recall that the x-coordinate of the vertex is also the axis of symmetry. Since a parabola is symmetric about the axis of symmetry, the axis of symmetry is halfway between the two roots.
From the equation, we can see that our two roots are x = 3 and x = -5.
Hence, the axis of symmetry or the x-coordinate of the vertex is:
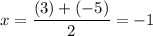
To find the y-coordinate of the vertex, evaluate the equation at x = -1:
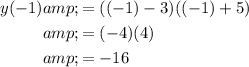
Hence, the vertex is at (-1, -16).