Answer:

Explanation:
We are given the equation:

And we want to find the value of k such that the equation has two real and equivalent roots.
Since the equation is a quadartic, we can find its discriminant (symbolized by Δ). Recall that:
- If Δ < 0, we have no real roots (two complex roots).
- If Δ > 0, we have two real roots.
- And if Δ = 0, we have one real root, or two equivalent ones.
First, rewrite our equation:
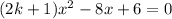
The discriminant is given by:
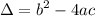
In this case, b = -8, a = (2k + 1), and c = 6.
Therefore, the discriminant is given by:

For it to have two equal roots, the discriminant must be zero. Hence:
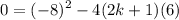
Solve for k:

Hence, the value of k is 5/6.