Question

Set A and the universal set U are defined as follows.

U={1,2,3,4,5,6)
A= {2,4,6}
Find the following sets.
Write your answer in roster form or as Ø.

Answer 1

Part (a)

Answer: Ø

This is the empty set

------------------

Step-by-step explanation:

It doesn't matter what set A is composed of. Intersecting any set with the empty set Ø will always result in the empty set.

This is because we're asking the question: "What does some set A and the empty set have in common?". The answer of course being "nothing" because there's nothing in Ø. Not even the value zero is in this set.

We can write Ø as { } which is a set of curly braces with nothing inside it.

=========================================================

Part (b)

Answer: {1,2,3,4,5,6}

-----------------

Step-by-step explanation:

When you union the universal set with any other set, you'll get the universal set.

The rule is
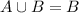`A \cup B = B` where I've made B the universal set to avoid confusion of the letter U and the union symbol
`\cup` which looks nearly identical.

Why does this rule work? Well if an item is in set
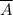`\overline{A}`, then it's automatically in set U (everything is in set U; it's the universe). So we're not adding anything to the universe when applying a union involving this largest set.

It's like saying

• A = set of stuff inside a persons house
• 
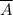  `\overline{A}` = set of stuff outside a persons house (ie stuff that is not in set A)
• U = set of every item

we can see that
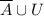`\overline{A} \cup U` will basically form the set of every item, aka the universal set.