Answer: Choice D
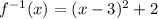
============================================================
Step-by-step explanation:
First we replace f(x) with y. This is because both y and f(x) are outputs of a function.
To find the inverse, we swap x and y and solve for y like so
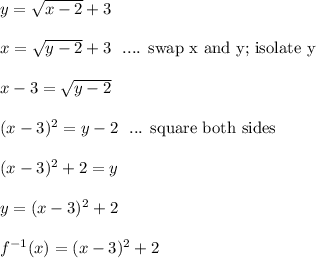
Note: because the range of the original function is
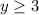 , this means the domain of the inverse is
, this means the domain of the inverse is
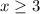 . The domain and range swap roles because of the swap of x and y.
. The domain and range swap roles because of the swap of x and y.
As the graph shows below, the original and its inverse are symmetrical about the mirror line y = x. One curve is the mirror image of the other over this dashed line.