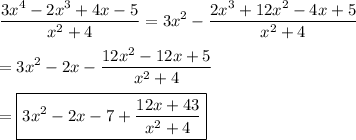Question

Divide (3x^4-2x^3+4x-5) / (x^2+4)

Answer 1

3x ⁴ = 3x ² • x ². Then

(3x ⁴ - 2x ³ + 4x - 5) - 3x ² (x ² + 4) = -2x ³ - 12x ² + 4x - 5

-2x ³ = -2x • x ². Then

(-2x ³ - 12x ² + 4x - 5) - (-2x) (x ² + 4) = -12x ² + 12x - 5

-12x ² = -12 • x ². Then

(-12x ² + 12x - 5) - (-12) (x ² + 4) = 12x + 43

So we've shown

`\displaystyle (3x^4-2x^3+4x-5)/(x^2+4) = 3x^2 - (2x^3+12x^2-4x+5)/(x^2+4) \\\\ = 3x^2 - 2x - (12x^2-12x+5)/(x^2+4) \\\\ = \boxed{3x^2 - 2x - 7 + (12x+43)/(x^2+4)}`