Answer:
y = -
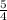 x + 8
x + 8
Explanation:
The perpendicular bisector intersects the line segment at its midpoint and is perpendicular to it.
Using the midpoint formula
M = (
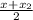 ,
,
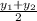 )
)
with (x₁, y₁ ) = (- 1, - 1) and (x₂, y₂ ) = (9, 7)
midpoint = (
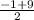 ,
,
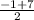 ) = (
) = (
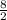 ,
,
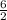 ) = (4, 3 )
) = (4, 3 )
Calculate the slope using the slope formula
m =
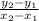
with (x₁, y₁ ) = (- 1, - 1) and (x₂, y₂ ) = (9, 7)
m =
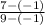 =
=
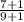 =
=
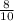 =
=
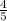
Given a line with slope m then the slope of a line perpendicular to it is
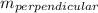 = -
= -
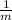 = -
= -
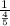 = -
= -
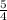 , then
, then
y = -
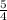 x + c ← is the partial equation
x + c ← is the partial equation
To find c substitute (4, 3) into the partial equation
3 = - 5 + c ⇒ c = 3 + 5 = 8
y = -
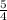 x + 8 ← equation of perpendicular bisector
x + 8 ← equation of perpendicular bisector