We're given
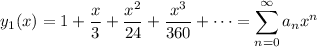
so let's see if we can find a closed form for the n-th term's coefficient.
Notice that
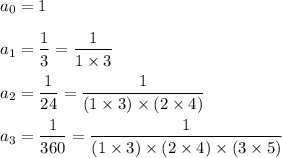
If the pattern continues, the next few terms are likely
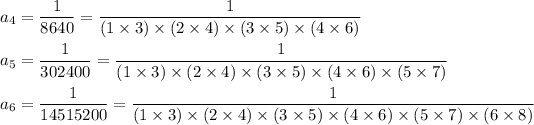
which leads up to the n-th term,
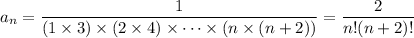
where the numerator is multiplied by 2 in order to "complete" the factorial pattern in (n + 2)!.
So we have
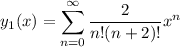
Now we use reduction of order to find a linearly independent solution of the form
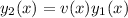 , with derivatives
, with derivatives
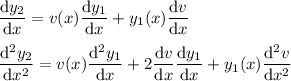
Substitute
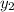 and its derivatives into the DE, and simplify the resulting expression to get a DE in terms of v(x) :
and its derivatives into the DE, and simplify the resulting expression to get a DE in terms of v(x) :
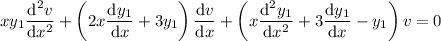
but since we know
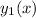 satisfies the original DE, the last term vanishes and we're left with
satisfies the original DE, the last term vanishes and we're left with
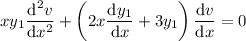
Reduce the order by substituting
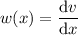 to get yet another DE in w(x) :
to get yet another DE in w(x) :
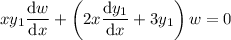
This equation is separable:
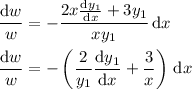
From here you would integrate to solve for w(x), then integrate again to solve for v(x), and finally for
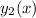 by multiplying
by multiplying
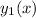 by v(x). Using the fundamental theorem of calculus, you would find
by v(x). Using the fundamental theorem of calculus, you would find
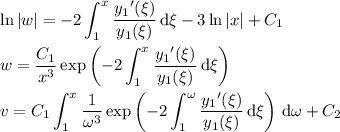
so that you end up with
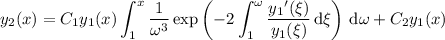
But the second term is already accounted for by
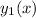 itself, so the second solution is
itself, so the second solution is
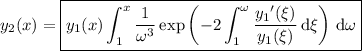
You could go the extra mile and try to find a power series expression for this solution, but that's a lot of work for little payoff IMO.