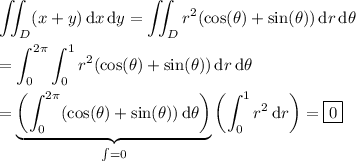Question

∫∫(x+y)dxdy ,d là miền giới hạn bởi x²+y²=1

Answer 1

It looks like you want to compute the double integral

`\displaystyle \iint_D (x+y) \,\mathrm dx\,\mathrm dy`

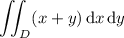
over the region D with the unit circle x ² + y ² = 1 as its boundary.

Convert to polar coordinates, in which D is given by the set

D = {(r, θ) : 0 ≤ r ≤ 1 and 0 ≤ θ ≤ 2π}

and

x = r cos(θ)

y = r sin(θ)

dx dy = r dr dθ

Then the integral is

`\displaystyle \iint_D (x+y)\,\mathrm dx\,\mathrm dy = \iint_D r^2(\cos(\theta)+\sin(\theta))\,\mathrm dr\,\mathrm d\theta \\\\ = \int_0^(2\pi) \int_0^1 r^2(\cos(\theta)+\sin(\theta))\,\mathrm dr\,\mathrm d\theta \\\\ = \underbrace{\left( \int_0^(2\pi)(\cos(\theta)+\sin(\theta))\,\mathrm d\theta \right)}_(\int = 0) \left( \int_0^1 r^2\,\mathrm dr \right) = \boxed{0}`