Question

Could someone please assist...it would really help alot...thank you:)

I just need help with 4.2 and 4.3​

Answer 1

Problem 4.2

We're told that y = 2x is the equation of the tangent line through point Q.

Plug this into the equation of the circle (that was given at the very top of the page). Solve for x.

x^2 + y^2 - 18x - 6y + 45 = 0

x^2 + (2x)^2 - 18x - 6(2x) + 45 = 0 ... every "y" replaced with "2x"

x^2 + 4x^2 - 18x - 12x + 45 = 0

5x^2 - 30x + 45 = 0

5(x^2 - 6x + 9) = 0

5(x-3)^2 = 0

(x-3)^2 = 0

x-3 = 0

x = 3

This then means y = 2x = 2*3 = 6

The coordinates of point Q are (x,y) = (3,6)

----------

Answer: (3,6)

===========================================================

Problem 4.3

We first need to find the location of point S. That will involve solving this system of equations

`\begin{cases}x-2y+12=0\\y = 2x\end{cases}`

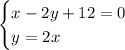
which represent the equations of lines SR and QS in that exact order.

Like before, we'll apply substitution to solve for x.

x-2y+12 = 0

x-2(2x)+12 = 0

x-4x+12 = 0

-3x+12 = 0

12 = 3x

12/3 = x

4 = x

x = 4

Which leads to y = 2x = 2*4 = 8

Point S is located at (4,8)

Point R is given to be located at (6,9)

Apply the distance formula for these two points to find the length of SR (aka the distance from S to R).

`S = (x_1,y_1) = (4,8)\\\\R = (x_2,y_2) = (6,9)\\\\d = \text{Length of SR, aka distance from S to R}\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((4-6)^2 + (8-9)^2)\\\\d = √((-2)^2 + (-1)^2)\\\\d = √(4 + 1)\\\\d = √(5)\\\\d \approx 2.236068\\\\`

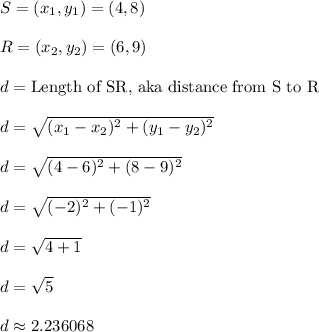
The exact length is
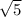`√(5)` and that approximates to roughly 2.236068 units.

----------

Answer:

Exact length =
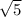`√(5)` units

Approximate length = 2.236068 units