Domain of a any cubic function
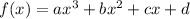 is defined to be always
is defined to be always
 .
.
The derivative with respect to x of your cubic function is,
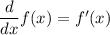
to find the derivative of a polynomial function, simply take a derivative of each factor and sum them up,
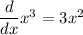 by the rule
by the rule
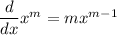 where
where
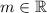
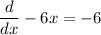

So the derivative is,
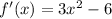
both derivative and the original function have equal domain.
Hope this helps :)