Question

If the nth term of A.P. are 7, 12, 17, 22.....is equal to the nth term of another A.P. 27, 30, 33, 36. Find the value of n?​

Answer 1

`n = 11`

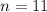
Explanation:

We are given two arithmetic sequences:

7, 12, 17, 22... and 27, 30, 33, 36...

And we want to determine n such that the nth term of each sequence is equivalent.

We can write a direct formula for each sequence. Recall that the direct formula for an arithmetic sequence is given by:

`\displaystyle x_n = a + d(n-1)`

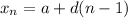
Where a is the initial term and d is the common difference.

The first sequence has an initial term of 7 and a common difference of 5. Hence:

`\displaystyle x_n = 7 + 5(n-1)`

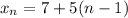
The second sequence has an initial term of 27 and a common difference of 3. Hence:

`x_n = 27 + 3(n-1)`

Set the two equations equal to each other:

`7 + 5 (n-1) = 27 + 3(n-1)`

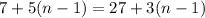
Solve for n. Distribute:

`7 + (5n - 5) = 27 + (3n - 3)`

Combine like terms:

`5n + 2 = 3n + 24`

Isolate:

`2n = 22`

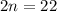
Divide. Hence:

`n = 11`

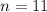
In conclusion, the 11th term of the first A.P. is equivalent to the 11th term of the second.