Answer:
B
Explanation:
Since we know the measure of ∠B and the side opposite to ∠B and we want to find BC, which is adjacent to ∠B, we can use the tangent ratio. Recall that:
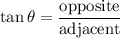
The angle is 54°, the opposite side measures 16 units, and the adjacent side is BC. Substitute:

Solve for BC. We can take the reciprocal of both sides:
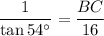
Multiply:
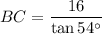
Use a calculator. Hence:

BC measures approximately 11.62 units.
Our answer is B.