Step-by-step explanation:
We will assume that the rim of the wheel is also very thin, like the spokes. The distance s between the spokes along the rim is
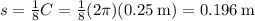
The 20-cm arrow, traveling at 6 m/s, will travel its length in
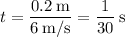
The fastest speed that the wheel can spin without clipping the arrow is
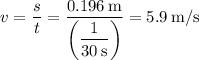
The angular velocity
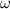 of the wheel is given by
of the wheel is given by
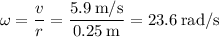
In terms of rev/s, we can convert the answer above as follows:
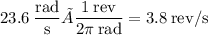
As you probably noticed, I did the calculations based on the assumption that I'm aiming for the edge of the wheel because this is the part of the wheel where a point travels a longer linear distance compared to ones closer to the axle, thus giving the arrow a better chance to pass through the wheel without getting clipped by the spokes. If you aim closer to the axle, then the wheel needs to spin slower to allow the arrow to get through without hitting the spokes.