Answer:
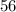 choices
choices
Explanation:
We know that we'll have to solve this problem with a permutation or a combination, but which one do we use? The answer is a combination because the order in which the child picks the candy does not matter.
To further demonstrate this, imagine I have 4 pieces of candy labeled A, B, C, and D. I could choose A, then C, then B or I could choose C, then B, then A, but in the end, I still have the same pieces, regardless of what order I pick them in. I hope that helps to understand why this problem will be solved with a combination.
Anyways, back to the solving! Remember that the combination formula is
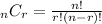 , where n is the number of objects in the sample (the number of objects you choose from) and r is the number of objects that are to be chosen.
, where n is the number of objects in the sample (the number of objects you choose from) and r is the number of objects that are to be chosen.
In this case,
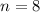 and
and
 . Substituting these values into the formula gives us:
. Substituting these values into the formula gives us:
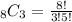
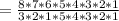 (Expand the factorials)
(Expand the factorials)
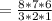 (Cancel out
(Cancel out
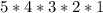 )
)
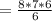 (Evaluate denominator)
(Evaluate denominator)
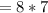 (Cancel out
(Cancel out
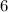 )
)
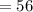
Therefore, the child has
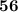 different ways to pick the candies. Hope this helps!
different ways to pick the candies. Hope this helps!