Question

Water flows into a right cylindrical shaped swimming pool with a circular base at a rate of 4 m33/min. The radius of the base is 3 m. How fast is the water level rising inside the swimming pool? The volume of a right cylinder with a circular base is V=πr2hV=πr2h, where rr is the radius of the base and hh is the height of the cylinder.

Answer 1

The water level is rising at a rate of approximately 0.1415 meters per minute.

Explanation:

Water is flowing into a right cylindrical-shaped swimming pool at a rate of 4 cubic meters per minute. The radius of the base is 3 meters.

And we want to determine the rate at which the water level of the pool is rising.

Recall that the volume of a cylinder is given by:

`\displaystyle V = \pi r^ 2h`

Since the radius is a constant 3 meters:

`\displaystyle V = 9\pi h`

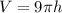
Water is flowing at a rate of 4 cubic meters per minute. In other words, dV/dt = 4 m³ / min.

Take the derivative of both sides with respect to t:

`\displaystyle (d)/(dt)\left[ V\right] = (d)/(dt)\left[ 9\pi h\right]`

Implicitly differentiate:

`\displaystyle (dV)/(dt) = 9\pi (dh)/(dt)`

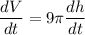
The rate at which the water level is rising is represented by dh/dt. Substitute and solve:

`\displaystyle \left(4 \right) = 9\pi (dh)/(dt)`

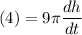
Therefore:

`\displaystyle (dh)/(dt) = (4)/(9\pi) \approx 0.1415\text{ m/min}`

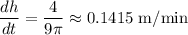
In conclusion, the water level is rising at a rate of approximately 0.1415 meters per minute.