Answer:
x = 5
Explanation:
We have
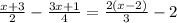
We can start by expanding the 2(x-2) into 2x-4
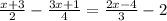
Next, we can remove denominators. We can start by multiplying both sides by 4. We do this because 2 (another denominator) is a factor of 4, so multiplying by 4 will remove both the denominator of 2 and the denominator of 4, resulting in
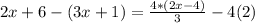
We can then simplify and expand
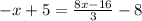
We can then multiply both sides by 3 to remove the other denominator
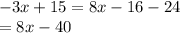
We then have
-3x+15 = 8x-40
We can start by adding 3x to both sides to make all the x values and their coefficients on one side, resulting in
15 = 11x - 40
We can then add 40 to both sides to isolate the x values and their coefficients, resulting in
55 =11x
We can finally divide both sides by 11 to isolate x
x = 55/11 = 5