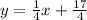Question

PLEASE HELP ASAP! NO SCAMS!

Answer 1

Explanation:

Perpendicular means that the slopes of the "old" line and the "new" line are opposite reciprocals; bisector means that the "new" line goes directly through the center of the "old" line. This perpendicular bisector, then, will go directly through the center of the "old" line, cutting it directly in half and leaving in its wake a 90 degree angle. To write this equation, then, of the perpendicular bisector, we need the slope of the old line and the midpoint of the old line. Let's work on the midpoint first:

`M=((3+6)/(2),(5-7)/(2))\\M=((9)/(2),(-2)/(2))\\M=((9)/(2),-1)` So the "new" line will go through this point.

Onto the slope:

`m=(-7-5)/(6-3)\\m=(-12)/(3)`so the slope is

m = -4. That means that the perpendicular slope is

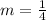`m=(1)/(4)` Now we're ready to write the equation:

`y-5=(1)/(4)(x-3)` and

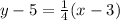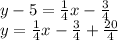`y-5=(1)/(4)x-(3)/(4)\\y=(1)/(4)x-(3)/(4)+(20)/(4)` and finally,

`y=(1)/(4)x+(17)/(4)`

Answer 2

Explanation:

A(3, 5) ; B(6,-7)

Let's find the slope of AB =
`(y_(2)-y_(1))/(x_(2)-x_(1))\\`

`=(-7-5)/(6-3)\\\\=(-12)/(3)\\\\= - 4`

m = -4

Slope of the perpendicular line to AB = -1/m =
`(-1)/(-4)=(1)/(4)`

The perpendicular line of AB is bisector also. So, it goes through the midpoint of AB

Midpoint of AB =
`((x_(1)+x_(2))/(2), (y_(2)-y_(1))/(2))`

`=((3+6)/(2),(5+(-7))/(2))\\\\=((9)/(2),(-2)/(2))\\\\=((9)/(2),-1)`

Equation of require perpendicular line: y - y1 = m (x -x1)

`(x_(1),y_(1))= ((9)/(2),-1)\\ \\m =(1)/(4)\\\\y-[-1]=(1)/(4)(x-(9)/(2))\\\\y+1=(1)/(4)x-(1)/(4)*(9)/(2)\\\\y=(1)/(4)x-(9)/(8)-1\\\\y=(1)/(4)x-(9)/(8)-(8)/(8)\\\\y=(1)/(4)x-(17)/(8)`