Answer:
see explanation
Explanation:
Given
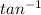 x +
x +
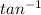 y +
y +
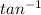 z = π
z = π
let
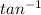 x = A ,
x = A ,
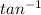 y = B ,
y = B ,
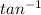 z = C , so
z = C , so
x = tanA, y = tanB , z = tanC
Substituting values
A + B + C = π ( subtract C from both sides )
A + B = π - C ( take tan of both sides )
tan(A + B) = tan(π - C) = - tanC ( expand left side using addition identity for tan )
 = - tanC ( multiply both sides by 1 - tanAtanB )
= - tanC ( multiply both sides by 1 - tanAtanB )
tanA + tanB = - tanC( 1 - tanAtanB) ← distribute
tanA+ tanB = - tanC + tanAtanBtanC ( add tanC to both sides )
tanA + tanB + tanC = tanAtanBtanC , that is
x + y + z = xyz