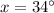Answer:
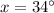
Explanation:
Note that ∠TSU and ∠PSR are vertical angles. Hence:
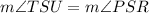
∠PSR is the sum of ∠PSQ and ∠QSR. Hence:
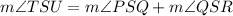
We know that ∠TSU measures 4x and ∠QSR measures 3x. Thus:
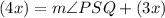
Solve for ∠PSQ:
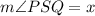
Next, ∠PQS and ∠RQS form a linear pair. Thus:
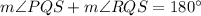
∠RQS measures 68°. Thus:
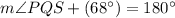
Solve for ∠PQS:
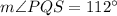
The interior angles of a triangle must total 180°. So, for ΔPQS:
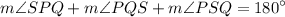
Substitute in the known values:
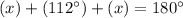
Simplify:
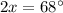
And divide. Hence: