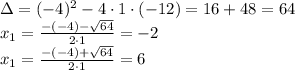Question

For which set of values of X is the algebraic expression x^2 - 16 over x^2 -4x - 12 undefined.

Answer 1

Explanation:

In order to be undefined, the fraction must have the denominator equal to 0, therefore we need to solve the equation

`x^2 -4x - 12 = 0\\`

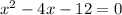
This is a second degree equation, and we can re-write it to

`(x-6)(x+2) = 0`

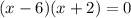
We notice that the solution to be composed of 2 values:

x = 6

and

x = -2

Therefore the set of values of x for which the said expression is undefined is

S={-2, 6}

Alternatively, if you don't notice how to re-write it factored, you can use the 2nd degree equation solving algorithm:

`\Delta = (-4)^2 - 4\cdot1\cdot(-12) = 16+48 = 64\\x_1 = (-(-4)-√(64) )/(2\cdot1) = -2\\x_1 = (-(-4)+√(64) )/(2\cdot1) = 6`