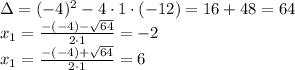Answer:
Explanation:
In order to be undefined, the fraction must have the denominator equal to 0, therefore we need to solve the equation
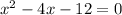
This is a second degree equation, and we can re-write it to
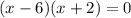
We notice that the solution to be composed of 2 values:
x = 6
and
x = -2
Therefore the set of values of x for which the said expression is undefined is
S={-2, 6}
Alternatively, if you don't notice how to re-write it factored, you can use the 2nd degree equation solving algorithm: