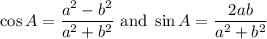Question

If tanA=2ab/a square-b square.find the value of cosA and sin A​

Answer 1

Explanation:

`sec^2A-tan^2A=1\\sec^2A=1+tan^2A=1+(4a^2b^2)/((a^2-b^2)^2) =((a^2-b^2)^2+4a^2b^2)/((a^2-b^2)^2) =((a^2+b^2)^2)/((a^2-b^2)^2) \\cos^2A=((a^2-b^2)^2)/((a^2+b^2)^2) \\cos A=(a^2-b^2)/(a^2+b^2) \\sin A=√(1-cos^2A) =\sqrt{1-((a^2-b^2)/(a^2+b^2) )^2} =\sqrt{((a^2+b^2)^2-(a^2-b^2)^2)/((a^2+b^2)^2) } =\sqrt{(4a^2b^2)/((a^2+b^2)^2) }=(2ab)/(a^2+b^2)`

Answer 2

`\displaystyle \displaystyle \cos A = (a^2-b^2)/(a^2 + b^2)\text{ and } \sin A = (2ab)/(a^2 + b^2)`

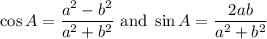
Explanation:

We are given that:

`\displaystyle \tan A = (2ab)/(a^2 - b^2)`

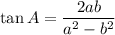
And we want to find the value of cos(A) and sin(A).

Recall that tangent is the ratio of the opposite side to the adjacent side.

Therefore, the opposite side measures 2ab, and the adjacent side measures a² - b².

Using the Pythagorean Theorem, solve for the hypotenuse:

`\displaystyle \begin{aligned} c^2 &= a^2 + b^2 \\ \\ c&= √((2ab)^2 + (a^2-b^2)) \\ \\ &= √((4a^2b^2)+(a^4-2a^2b^2+b^4)) \\ \\ &= √(a^4 + 2a^2b^2 + b^4 ) \\ \\ &= √((a^2 +b^2)^2) \\ \\ &= a^2 + b^2\end{aligned}`

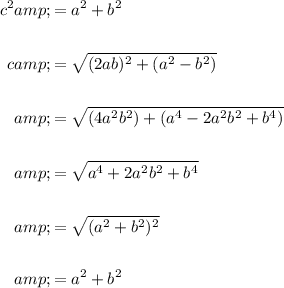
Thus, our hypotenuse is given by a² + b².

Cosine is the ratio between the adjacent side and the hypotenuse. Thus:

`\displaystyle \cos A = (a^2-b^2)/(a^2 + b^2)`

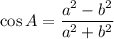
And sine is the ratio between the opposite side and the hypotenuse. Thus:

`\displaystyle \sin A = (2ab)/(a^2 + b^2)`

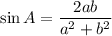
In conclusion:

`\displaystyle \displaystyle \cos A = (a^2-b^2)/(a^2 + b^2)\text{ and } \sin A = (2ab)/(a^2 + b^2)`