Answer:
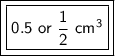
Step-by-step explanation:
We are asked to find the volume of a solid given the density and mass. The formula for density is:
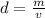
We know the solid's density is 14 grams per cubic centimeter and the mass is 7 grams.
Substitute the known values into the formula.
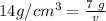
We are solving for the volume of the solid, so we must isolate the variable v. First, cross multiply. Multiply the first numerator by the second denominator, then the first denominator and second numerator.
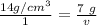
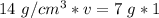
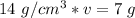
Now the variable is being multiplied by 14 grams per cubic centimeters. The inverse operation of multiplication is division, so we divide both sides by 14 g/cm³.
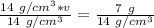
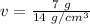
The units of grams cancel.
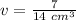
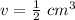
The volume of the solid is 1/2 or 0.5 cubic centimeters.