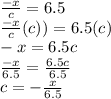Question

-x/c=6.5
I need to solve for x first then c

Answer 1

x = -6.5c

-x/6.5 = c

Explanation:

-x/c=6.5

Multiply each side by -c

-x/c * -c=6.5*-c

x = -6.5c

-x/c=6.5

Multiply each side by c

-x/c *c=6.5*c

-x = 6.5c

Divide each side by 6.5

-x/6.5 = 6.5c/6.5

-x/6.5 = c

Answer 2

`x = -6.5c`

`c = -(x)/(6.5)`

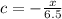
Explanation:

In both cases, you are simply isolating the variable you are trying to solve for:

`(-x)/(c) = 6.5`

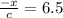
Solve for x. Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. First, multiply c to both sides, and then divide -1 from both sides:

`(-x)/(c) = 6.5\\(-x)/(c) * c = 6.5 * c\\-x = 6.5c\\(-x)/(-1) = (6.5c)/(-1)\\x = -6.5c`

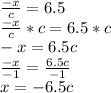
Solve for c. Isolate the variable, c. Note the equal sign, what you do to one side, you do to the other. Multiply -1/x to both sides of the equation:

`(-x)/(c) = 6.5\\(-x)/(c)(c)) = 6.5(c) \\-x = 6.5c\\(-x)/(6.5) = (6.5c)/(6.5)\\c = -(x)/(6.5)`