Question

A triangle has sides with lengths of 6 inches, 8 inches, and 11 inches. Is it a right triangle

Answer 1

NO.

Explanation:

If it is a right triangle then if h = longest side then by the inverse of Pythagoras Theorem:

h^2 = a^2 + b^2 (where a and b are other 2 sides).

So with the given values:

h^2 = 11^2 = 121

a^2 + b^2 = 6^2 + 8^2 = 36 + 64 = 100.

-not equal so NOT a right triangle.

Answer 2

No

Explanation:

In every right triangle,
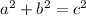`a^(2) +b^2=c^2` where "a" and "b" are the legs of the right triangle and "c" is the hypotenuse (This is known as "Pythagorean's theorem). To figure out if a triangle with side lengths 6, 8, and 11 inches is a right triangle, all you have to do is plug in the values 6 and 8 for "a" and "b" and the value 11 for "c" to get":

`6^2+8^2=11^2`

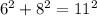
This simplifies to:

`36+64=121`

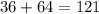
Which simplifies further to:

`100=121`

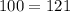
This is obviously incorrect so therefore, the triangle lengths given do not form a right triangle.

Hope this helps :)