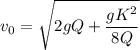Step-by-step explanation:
Recall that

and

From Eqn(2), we can write
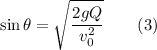
Using the identity
 , we can rewrite Eqn(1) as
, we can rewrite Eqn(1) as
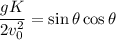
Squaring the above equation, we get
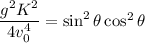
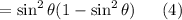
Use Eqn(3) on Eqn(4) and we will get the following:
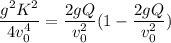
This simplifies to
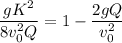
Rearranging this further, we get
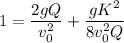
Putting
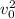 to the left side, we get
to the left side, we get
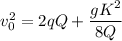
Finally, taking the square root of the equation above, we get the expression for the muzzle velocity
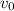 as
as