Answer:
Part A)
0.1 liters per minute.
Part B)
There was initially 3.8 liters of water.
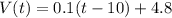
Part C)
562 minutes.
Explanation:
A tank is filled at a constant rate. After 10 minutes, the tank contains 4.8 L of water and after 35 minutes, the tank contains 7.3 L of water.
Part A)
We can represent the current data with two points: (10, 4.8) and (35, 7.3). The x-coordinate is measured in minutes since the tank began to be filled and the y-coordinate is measured in how full the tank is in liters.
To find the rate at which the tank is being filled, find the slope between the two points:
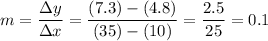
In other words, the rate at which the tank is being filled is 0.1 liters per minute.
Part B)
To find the function of the volume of the tank, we can use the point-slope form to first find its equation:
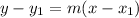
Where m is the slope/rate of change and (x₁, y₁) is a point.
We will substitute 0.1 for m and let (10, 4.8) be the point. Hence:
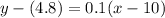
Simplify:
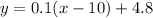
Since y represent how full the tank is and x represent the time in minutes since the tank began to be filled, we can substitute y for V(t) and x for t. Thus, our function is:
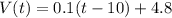
The initial volume is when t = 0. Evaluate:

There was initially 3.8 liters of water.
Part C)
To find how long it will take for the tank to be completely filled given its maximum capacity of 60 liters, we can let V(t) = 60 and solve for t. Hence:
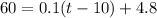
Subtract:
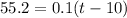
Divide:
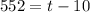
Add. Therefore:
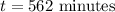
It will take 562 minutes for the tank to be completely filled.