Answer:
About 1.85 seconds and 13.15 seconds.
Explanation:
The height (in feet) of the rocket t seconds after launch is given by the equation:
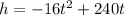
And we want to determine how many seconds after launch will be rocket be 390 feet above the ground.
Thus, let h = 390 and solve for t:

Isolate:
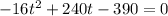
Simplify:
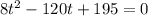
We can use the quadratic formula:
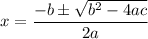
In this case, a = 8, b = -120, and c = 195. Hence:
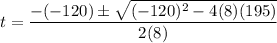
Evaluate:
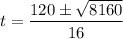
Simplify:
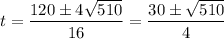
Thus, our two solutions are:

Hence, the rocket will be 390 feet above the ground after about 1.85 seconds and again after about 13.15 seconds.