Answer:
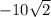
Explanation:
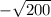
To factor an integer, we need to repeatedly divide it by the ascending sequence of primes (2, 3, 5)
In the end, the number of times each prime divides the original integer becomes its exponent.
Prime number 2 to the power of 3 equals 8, and 5 to the power of 2 equals 25.
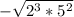
We need to rewrite certain factors as the product of two factors in order to remove them from the radical.
The exponent of the first factor in such a product will be equally divided by the radical index, allowing us to eliminate it from the radical.
Here, because their exponents are evenly divided by the radical index, we will be able to eliminate the following components from the radical:
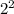 and
and
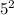

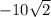
OAmalOHopeO