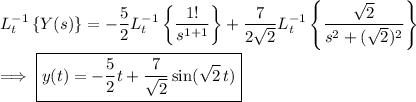Question

Use the Laplace transform to solve the given system of differential equations. d2x dt2 + x − y = 0 d2y dt2 + y − x = 0 x(0) = 0, x'(0) = −6, y(0) = 0, y'(0) = 1

Answer 1

I'm going to assume that "−" is supposed to be some kind of minus character, so that the given system of DEs is supposed to be

`\begin{cases}(\mathrm d^2x)/(\mathrm dt^2) + x - y = 0 \\ (\mathrm d^2y)/(\mathrm dt^2) + y - x = 0 \\ x(0) = 0, x'(0) = -6, y(0) = 0, y'(0) = 1\end{cases}`

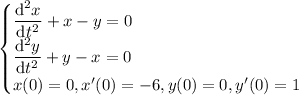
Take the Laplace transform of both sides of both equations. Recall the transform for a second-order derivative,

`L_s\left\{(\mathrm d^2f(t))/(\mathrm dt^2)\right\} = s^2 F(s) - sf(0) - f'(0)`

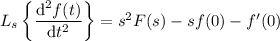
where F(s) denotes the transform of f(t). You end up with

`\begin{cases}s^2X(s)-sx(0)-x'(0) + X(s) - Y(s) = 0 \\ s^2Y(s) - sy(0) - y'(0) + Y(s) - X(s) = 0\end{cases} \\\\ \begin{cases}(s^2+1)X(s) - Y(s) = -6 \\ (s^2+1)Y(s) - X(s) = 1\end{cases}`

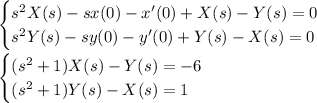
and solving for X(s) and Y(s) (nothing tricky here, just two linear equations) gives

`X(s) = -(6s^2+5)/(s^2(s^2+2)) \text{ and } Y(s) = (s^2-5)/(s^2(s^2+2))`

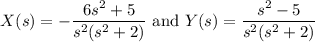
Now solve for x(t) and y(t) by computing the inverse transforms. To start, split up both X(s) and Y(s) into partial fractions.

• Solving for x(t) :

`-(6s^2+5)/(s^2(s^2+2)) = \frac as + \frac b{s^2} + (cs+d)/(s^2+2) \\\\ -6s^2-5 = as(s^2+2) + b(s^2+2) + (cs+d)s^2 \\\\ -6s^2-5 = (a+c)s^3 + (b+d)s^2 + 2as + 2b \\\\ \implies \begin{cases}a+c=0\\b+d=-6\\2a=0\\2b=-5\end{cases} \implies a=c=0, b=-\frac52, d=-\frac72`

`\implies X(s) = -\frac5{2s^2} - \frac7{2(s^2+2)}`

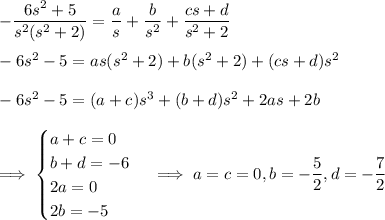
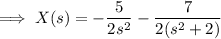
Taking the inverse transform, you get

`L^(-1)_t\left\{X(s)\right\} = -\frac52 L^(-1)_t\left\{(1!)/(s^(1+1))\right\} - \frac7{2\sqrt2} L^(-1)_t\left\{(\sqrt2)/(s^2+(\sqrt2)^2)\right\} \\\\ \implies \boxed{x(t) = -\frac52 t - \frac7{2\sqrt2}\sin(\sqrt2\,t)}`

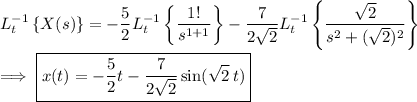
• Solving for y(t) :

`(s^2-5)/(s^2(s^2+2)) = \frac as + \frac b{s^2} + (cs+d)/(s^2+2) \\\\ s^2 - 5 = as(s^2+2) + b(s^2+2) + (cs+d)s^2 \\\\ s^2 - 5 = (a+c)s^3 + (b+d)s^2 + 2as + 2b \\\\ \implies \begin{cases}a+c=0\\b+d=1\\2a=0\\2b=-5\end{cases} \implies a=c=0, b=-\frac52, d=\frac72`

`\implies Y(s) = -\frac5{2s^2} + \frac7{2(s^2+2)}`

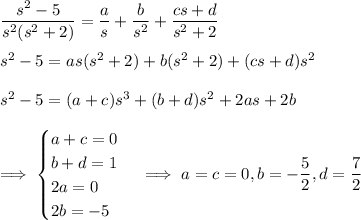
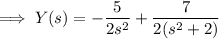
Inverse transform:

`L^(-1)_t\left\{Y(s)\right\} = -\frac52 L^(-1)_t\left\{(1!)/(s^(1+1))\right\} + \frac7{2\sqrt2} L^(-1)_t\left\{(\sqrt 2)/(s^2+(\sqrt2)^2)\right\} \\\\ \implies \boxed{y(t) = -\frac52 t + \frac7{\sqrt2} \sin(\sqrt2\,t)}`