Answer:
![\displaystyle [CQF]=5](https://img.qammunity.org/2022/formulas/mathematics/high-school/4gwxlvi2ndfbd6ou8365jbjbsg3wk5o5bi.png)
Explanation:
Note that
![[n]](https://img.qammunity.org/2022/formulas/mathematics/high-school/9mahnfvcurl2tfbbd4h18b0gbxas134jc6.png) refers to the area of some polygon
refers to the area of some polygon
 .
.
Diagonal
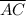 forms two triangles,
forms two triangles,
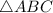 and
and
 . Both of these triangles have an equal area, and since the area of parallelogram
. Both of these triangles have an equal area, and since the area of parallelogram
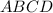 is given as
is given as
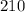 , each triangle must have an area of
, each triangle must have an area of
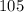 .
.
Furthermore,
 is broken up into two smaller triangles,
is broken up into two smaller triangles,
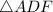 and
and
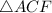 . We're given that
. We're given that
 . Since
. Since
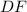 and
and
 represent bases of
represent bases of
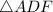 and
and
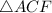 respectively and both triangles extend to point
respectively and both triangles extend to point
 , both triangles must have the same height and hence the ratio of the areas of
, both triangles must have the same height and hence the ratio of the areas of
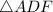 and
and
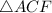 must be
must be
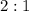 (recall
(recall
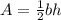 ).
).
Therefore, the area of each of these triangles is:
![[ACF]+[ADF]=105,\\[][ACF]+2[ACF]=105,\\3[ACF]=105,\\[][ACF]=35 \implies [ADF]=70](https://img.qammunity.org/2022/formulas/mathematics/high-school/7ltwm7dcicahf7aagv0bh2lleikdxyv9gf.png)
With the same concept, the ratio of the areas of
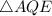 and
and
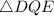 must be
must be
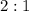 respectively, from
respectively, from
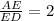 , and the ratio of the areas of
, and the ratio of the areas of
 and
and
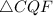 is also
is also
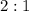 , from
, from
 .
.
Let
![[DQE]=y](https://img.qammunity.org/2022/formulas/mathematics/high-school/3z1643y15kxdaxllri37envd5plsgss8i9.png) and
and
![[CQF]=x](https://img.qammunity.org/2022/formulas/mathematics/high-school/kucd7dqghy54zy62pl4bqn7i94d4uofz02.png) (refer to the picture attached). We have the following system of equations:
(refer to the picture attached). We have the following system of equations:
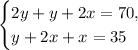
Combine like terms:
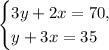
Multiply the second equation by
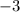 , then add both equations:
, then add both equations:
![\displaystyle \begin{cases}3y+2x=70,\\-3y-9x=-105\end{cases}\\\\\rightarrow 3y-3y+2x-9x=70-105,\\-7x=-35,\\x=[CQF]=(-35)/(-7)=\boxed{5}](https://img.qammunity.org/2022/formulas/mathematics/high-school/dr71gayc6xbq8yxzgsbkgs3htdb3cvmo97.png)