Question

Let a1, a2, . . . , a2019 be a sequence of real numbers. For every five indices i, j, k, `, and m from 1 through 2019, at least two of the numbers ai , aj , ak, a` , and am have the same absolute value. What is the greatest possible number of distinct real numbers in the given sequence

Answer 1

There are at most 4 distinct absolute values of elements taken from this sequence. (If there were at least 5 distinct absolute values, then you could pick
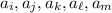`a_i,a_j,a_k,a_\ell,a_m` each with different absolute values, but that would contradict the given statement "for every five indices ... at least two of ... have the same absolute value".)

The pigeonhole principle then says that 2 of any 5 numbers taken from this sequence have the same absolute value. Both |x| = x and |-x| = x, so there can be at most 8 distinct numbers in the sequence.