Question

An astronaut is traveling in a space vehicle that has a speed of 0.480c relative to Earth. The astronaut measures his pulse rate at 78.5 per minute. Signals generated by the astronaut's pulse are radioed to Earth when the vehicle is moving perpendicularly to a line that connects the vehicle with an Earth observer. (Due to vehicle's path there will be no Doppler shift in the signal.)

(a) What pulse rate does the Earth-based observer measure? beats/min
(b) What would be the pulse rate if the speed of the space vehicle were increased to 0.940c?
beats/min

Answer 1

Step-by-step explanation:

The heart rate of the astronaut is 78.5 beats per minute, which means that the time between heart beats is 0.0127 min. This will be the time t measured by the moving observer. The time t' measured by the stationary Earth-based observer is given by

`t' = \frac{t}{\sqrt{1 - \left((v^2)/(c^2)\right)}}`

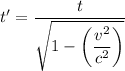
a) If the astronaut is moving at 0.480c, the time t' is

`t' = \frac{0.0127\:\text{min}}{\sqrt{1 - \left((0.2304c^2)/(c^2)\right)}}`

`\:\:\:\:=0.0145\:\text{min}`

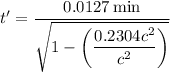
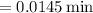
This means that time between his heart beats as measured by Earth-based observer is 0.0145 min, which is equivalent to 69.1 beats per minute.

b) At v = 0.940c, the time t' is

`t' = \frac{0.0127\:\text{min}}{\sqrt{1 - \left((0.8836c^2)/(c^2)\right)}}`

`\:\:\:\:=0.0372\:\text{min}`

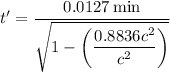
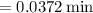
So at this speed, the astronaut's heart rate is 1/(0.0372 min) or 26.9 beats per minute.